GROVE: https://doi.org/10.1093/gmo/9781561592630.article.06186
Pythagoreïsche stemming en Pythagoreïsch komma 
Door de eeuwen heen is er door schrijvers over muziek en muziektheorie veel aandacht besteed aan snaarverdelingen, meestal geïllustreerd met behulp van het monochord.
Binnen de benadering van Pythagoras spelen de getallen 1, 2, 3 en 4 (ook wel tetraktys genaamd) een sleutelrol. De som van deze 4 is 10.

Toegepast op snaarverdeling (1, 1/2, 1/3, 1/4) leveren deze octaaf, reine kwint, reine kwart als intervallen op.
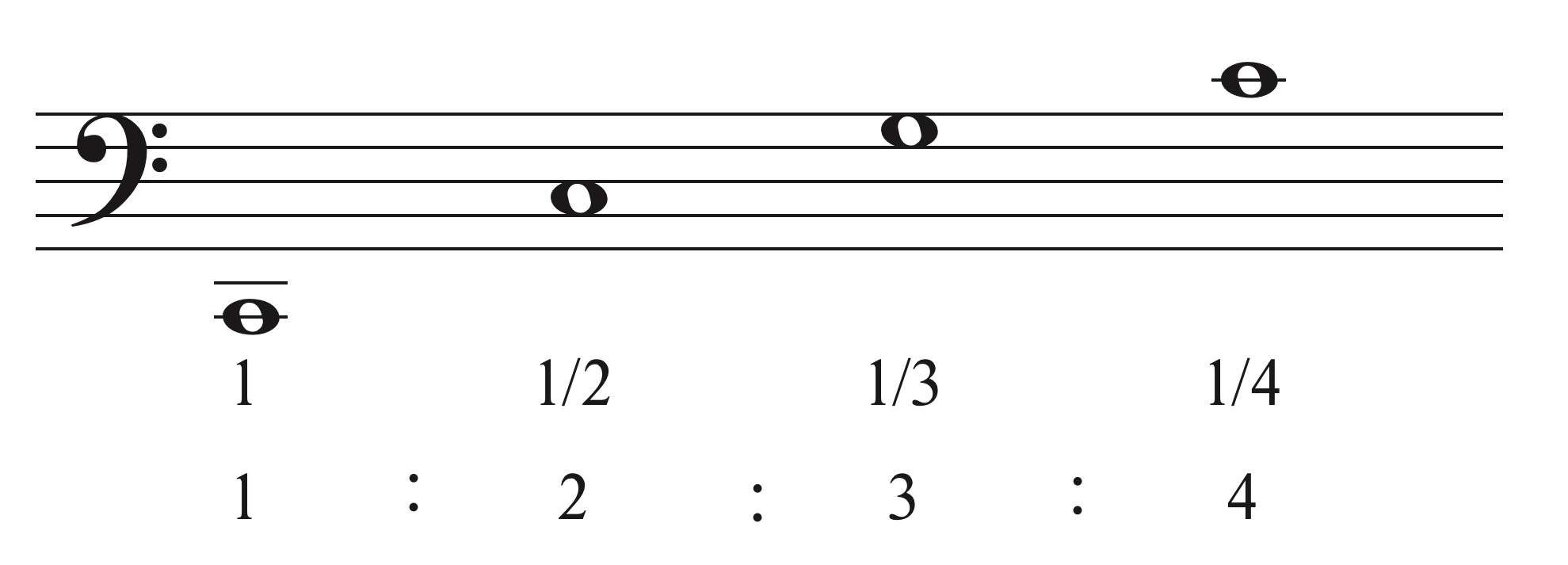
De frequenties van deze snaarlengtes verhouden zich als 1 : 2 : 3 : 4.
Vanuit deze verhoudingen is het mogelijk andere tonen af te leiden en op die manier toonvoorraden (ladders, modi) samen te stellen.
Het uitgangspunt is: werken met reine kwinten/kwarten en octaven; andere intervallen komen voort uit combinaties hiervan
Voorbeeld van een diatonische ladder:
C (basis snaarlengte)
c
G
d --> D
A
e --> E
B
c --> F
C-D-E-F-G-A-B-c
Construeren we een reeks van opeenvolgende kwinten dan ontstaat wat algemeen bekend is als de kwintencirkel.
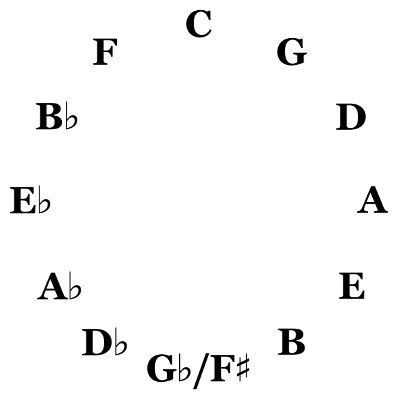
Een kwinten- of kwartencirkel levert alle 12 pitchclasses op.
Nu wil het geval dat een opeenvolging van 12 reine kwinten geen gesloten cirkel oplevert.
Pythagoreïsch komma
Een reeks van 12 reine kwinten keert niet terug op een zuiver octaaf van de begintoon, maar is beduidend hoger. Met andere woorden: B# ≠ C.
In deze context blijkt dat enharmonisch "gelijke" tonen helemaal niet gelijk zijn. Ze verschillen een (Pythagoreïsch) komma.
Dat is proefondervindelijk aan te tonen door zelf te stemmen, maar ook door het uit te rekenen:
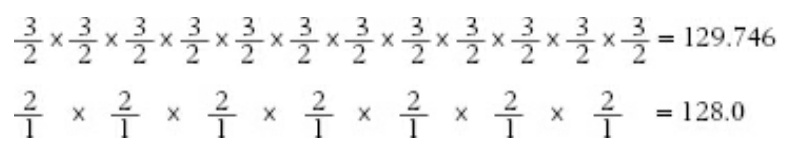
3/2 tot de macht 12 = 531441/4096 = 129,746338
2 tot macht 7 = 128
| C | G | D | A | E | B | F# | C# | G# | D# | A# | E# | B# |
| Fb | Cb | Gb | Db | Ab | Eb | Bb | F | C |
Binnen onze evenredig zwevende stemming is de laatste b# gelijk aan c, binnen de Pythagoreïsche stemming is er een duidelijk verschil tussen b# en c, deze tonen zijn enharmonsiche varianten, ze verschillen in toonhoogte.
De benaming enharmonisch gelijke tonen mag binnen de evenredig zwevende stemming (moderne piano's) opgaan, in de algemene muziekpraktijk ligt dat genuanceerder.
Pythagoreïsche grote terts
De grote terts die we afleiden uit 4 zuivere kwinten is voor ons gehoor onaangenaam te groot.
3/2 tot de macht 4 = 81/64.
De gegeven verhouding vanuit snaarverdeling zou zijn: 5/4 = 80/64
Dit verschil tussen een Pythagoreïsche en een zuivere terts noemen we een Didymisch komma. Een andere naam hiervoor is syntonisch komma.
De evenredig zwevende terts is beter dan de pythagoreïsche, maar niet zo zuiver als de reine grote terts.
Strijkers die tertsen en sexten spelen met dubbelgrepen, streven er naar de zwevingen uit de samenklank te krijgen, ze streven naar een zuivere intonatie of just intonation.



